티스토리 뷰

안녕하세요 :)
이번 포스팅에서 다루어볼 내용은 메모리 관리 입니다.
페이징 기법이니 세그먼테이션 기법이니 뭐니 사실 어려워요... 수업 들을때 잘 들어오지도 않는 내용을 우겨넣을라고 열심히 노력했던거 같네요! ㅎ 그래도 깔끔하게 정리해서 완벽히 제꺼로 만들기 위해 노력해보겠습니다.
이번 포스팅에서 다룰내용은 메모리에 관한 이야기 입니다. 사실 다음포스팅도 메모리에 관련된 이야기를 할것 같습니다. 메모리를 쪼개고 쪼갠거에 알맞게 프로세스를 올리고 할것인데요!!
그럼 도대체 메모리를 왜 쪼갤까요?
이유는 리소스의 효율을 높이고, 여러 프로세스를 올리기위해서 메모리를 분할하는것입니다...! 이제부터 메모리 관리와 여러가지 기법에 대해 다루며 메모리를 효율적으로 사용하기위해 운영체제가 어떤일을하는지 한번 알아가 보겠습니다. 알기 싫어도 시험보려면 알아봐야죠ㅎㅎ....
Memory Management Requirements (메모리 관리 요구사항)
relocation - 다시 위치시키는것입니다. 자리를 다시 이용해야 하는경우가 생기기 때문입니다
개발자는 프로그램이 메모리공간상 어느곳에 위치할지 모른다. 수행중에 다시 배치될수도 있다(swaping 으로 인해) 스와핑 지난 포스팅중 프로세스 상태 정보에 대한 포스팅에서 다루어 보았습니다.
주소값이 언제든 바뀔 가능성이 있습니다!
protection - 프로세스간의 권한이 인정되어야 한다는것 입니다. 함부로 참조해서는 안되는것이죠, 이 작업을 운영체제가 관여 하기에는 벅차기 때문에 하드웨어가 관장해줍니다.
sharing - 라이브러리와 같이 메모리관계에서 공유에 대한 매커니즘이 있어야 한다.
logical - 모듈링프로그램에서 사용할때, 다이나믹 링킹(dll) 파일 처럼 필요할때마다 유기적으로 연결된 실행코드를 사용한다.(마치 하나의 독립적인 소스처럼)
physical - HDD, 와 main 메모리 두가지 메모리가 사실 존재한다!
용어
Frame - A fixed length block of main memory, 메인메모리를 고정된 길이의 블럭으로 쪼갠 단위
Page A fixed length block of data that resides in secondary memory, 보조 기억장치를 고정된 블럭으러 쪼갠 단위
Segment A variable length block of data that resides in secondary memory, 보조 기억장치를 가변가능한 블럭으로 쪼갠 단위
Internal Fragmentation (내부 단편화)
메모리 할당시, 프로세스가 필요로 하는 양보다 더 많은 양이 할당 되었을때, 낭비되는 메모리 공간
External Fragmentation (외부 단편화)
메모리의 할당과 해제에 과정으로 인해 중간중간에 생기는 메모리 작은 영역, 디스크 조각모음을 하기 전 처럼 중간중간 틈이 생긴것
Memory Partitioning
fixed partitioning
시스템 설계시 메인메모리를 고정된 크기로 분할, 쪼개진 메모리에 프로세스를 올림, 파티션 사이즈 보다 작은 프로세스는 어디든 들어갈수 있음, 파티션한 공간이 full일시 swap하거나 기다린다.
- 고정된 파티션의 경우 내부 단편화, Internal Fragmentation가 발생할수 있다.
- 프로그램이 만약 파티션크기에 맞지 않는다면 프로그래머는 오버레이를 사용하여 프로그램을 설계해야 한다.
오버레이 - 사용가능한 주소 공간 이상의 프로그램을 작동하게 하는 프로그래밍 기법
Placement Algorithm with Partitions
여러개의 파티션중 프로그램을 어디에 배치할 것인가?
만약 똑같은 사이즈의 파티션이라면 고민할 필요없이 어디에 배치하던 똑같은 결과일것입니다.
각각 다른 사이즈를 갖는 파티션이라면 Placement Algorithm을 사용합니다. 프로그램 자기 자신 사이즈에 딱 알맞는 최소한 작은 파티션에 할당하는것입니다. 이때는 각각의 파티션이 각각의 잡큐를 사용합니다.
고정된 크기의 파티션 기법의 장점 - 구성과 구현이 간단하다0000000, 단점 - 파티션의 갯수에 따라 운용할수 있는 프로세스의 갯수가 정해진다. 작은 일을 하는데도 큰 용량을 소비할수 있다.
Dynamic Partitioning
-프로세스의 크기에 딱 맞게 파티셔닝 해주는 것입니다. 그런데 프로세스에게 메모리를 할당해주고 제거해주는 과정에서 어쩔수 없이 작은 구멍들을 만들어 내게 됩니다. 이것이 External Fragmentation (외부 단편화) 입니다
그렇기 때문에 자주자주 compaction(압축)을 수행해 주어야 합니다. 디스크 조각모음 같은것을 이야기 합니다.
Dynamic Partitioning Placement Algorithm
운영체제는 놀고있는 메모리 파티션을 프로세스에게 할당해 주어야 합니다. 이때 어느 위치에 할당해어야 하는가에 따라 세가지 알고리즘이 존재합니다.
1. Best fit algorithm
2. First fit algorithm
3. Next fit algorithm
Best fit algorithm
이름은 베스트라 하지만 성능면에서 최악인 알고리즘입니다. 프로세스가 필요한 메모리 사이즈에 딱 맞게 최소한으로 메모리 블럭을 할당해 주는 방법입니다. 이렇게 하면 이전에 언급한 External Fragmentation영역이 엄청나게 많아짐으로 compaction(압축)을 수행해주는 횟수도 빈번해집니다. 압축하는데 시간을 엄청할여해서 성능이 떨어지는것이죠
First fit algorithm
이 방법은 가장 심플하게 메모리의 가장 첫부분부터 검색해서 프로세스가 들어갈수있는 공간이 있다면 크기에 상관없이 바로바로 할당해주는 방법입니다. 가장 심플하고 빠른 방법입니다. 하지만 할당된 위치가 대부분 앞쪽으로 몰리게 됩니다. 그리고 여유공간이 어디에 위치하고 있던지 제일 앞부터 검색한다는점이 단점입니다.(만약 제일 마지막에 여유공간이 있다해도 제일 앞부분부터 순차적으로 검색해서 제일 마지막에 검색되겠죠)
Next fit
이 방법은 가장 마지막으로 사용한 메모리주소부터 검색을 시작해서 여유공간을 찾아내면 프로세스를 할당하는 방식입니다. 중간중간 작은 프로세스로 인해 쪼개진 영역탓에 큰 메모리를 요구할때 필요한 큰 블럭은 깨지게 되죠
메모리의 제일 마지막에 위치한 큰 블럭부터 컴펙션을 수행합니다.
Buddy System
fixed partition 과 dynamic partition을 혼합한 형태의 시스템입니다.
프로세스의 크기에 따라 2의 승수배 만큼 메모리를 쪼개어서 메모리를 할당해 주는 방법입니다.
만약 35비트 메모리를 필요로 한다면 2^5 와 2^6 사이의 범주에 들어가게 되는것입니다. 간단한 그림예제는 아래와 같습니다.

Relocation
만약 swapping 을 당한 프로세스나 compaction(압축)을 당한 프로세스는 원래 할당받은 주소가아닌 다른 주소로 재할당 되게 될 것입니다. 이에 대한 이해를 돕기 위해 주소에 대한 이야기를 조금 하겠습니다.
주소는 논리(Logical), 물리(Physical), 상대(Relative) 주소로 나뉩니다,
논리주소는 시스템상의 메모리 할당또는 연산을 위한 논리적인 주소이며 반드시 논리주소로 변환되어서 쓰입니다.
물리주소는 실제 시스템이 처리하는 실제 물리적 주소값입니다.
상대주소는 논리 주소의 일종으로 하나의 기준이되는 값으로부터의 상대적인 값이며, 실제로는 알려지지않은 주소입니다. 예를 들어 @+6 이라면 35를 할당해서 상대적 계산후 41이라는 상대주소를 갖는것입니다.
Registers Used during Execution(연산되는 동안 사용된 레지스터)
base register
-프로세스를 위한 스타팅 어드레스, 스와핑 및 컴팩션시 바뀔수 있음, PCB에 저장하는것이 좋음
bounds register
-프로세스를 위해 논리적으로 주소를 바꿔줌
프로세스가 올려질 마지막 주소를 bound라 칭할때, Relative+base 연산후 bound와 비교하는 연산을 이행합니다. 이때 값이 bound를 넘어갈시 인터럽트를 발생시킵니다.(물리적 메모리 영역보다 큰 프로세스를 올릴려고 시도했기 때문이겠죠)
이 값들은 프로세스가 로드되거나 스왑인 될때 설정됩니다.
배이스 레지스터의 값은 상대주소와 더해져 추상적인 주소로 생산됩니다.
결과 주소(resulting address)는 바운드레지스터와 소통합니다.
만약 주가 바운드와 같이 하지 않는다면, 인터럽트가 생기고 운영체제에게 전달됩니다.
+@ 실제 메모리 체계가 완벽히 위와 같지는 않지만 원리를 이해하기 위한것 입니다.
paging
제가 페이징 이라는 위 글씨에는 <h1>태그를 넣어 게시했습니다. 그만큼 많이 중요한 내용입니다.
페이징이란 메모리를 같은 사이즈의 덩어리로 쪼개고 각각의 프로세스를 같은 사이즈의 덩어리로 쪼개는것입니다.
(프로세스와 메모리를 같은사이즈의 덩어리로 쪼갠다? 그대로 메모리에 올리면 딱 맞게 올라가겠죠!)
이때 쪼개어진 프로세스 덩어리를 page, 쪼개어진 메모리 덩어리를 frame 이라 칭합니다...!
페이지를 표현할때는 논리주소, 프레임을 표현할때는 물리주소입니다.
앞으로 논리적인 주소로 포인팅된 페이지를 물리적인주소로 포인팅 된 프레임으로 바꾸는것을 생각해볼것입니다.
고정된 위치에 있는 프레임들에 프레임과 똑같은 사이즈로 이루어진 페이지들을 끼웠다 뺏다 하는거죠
근데 이 끼웠다 뺏다를 어떻게 매핑시킬까요? 페이지 테이블을 보고하는거입니다. 이제 알아보겠습니다.
운영체제는 각 프로세스에 대하여 페이지 테이블을 함유하고 있습니다.
페이지 테이블 - 각각의 페이지를 위한 프레임 위치를 프로세스 안에 포함하고 있습니다.
이제 메모리의 주소는 페이지 테이블과 함께 페이지 번호와 옵셋으로 구성됩니다 (Memory address consist of a page number and offset within the page)
No external fragmentation
쪼개진대로 딱 맞게 올라가니까 외부 단편화가 일어나지 않겠죠!
Assignment of Process Pages to Free Frames
이제 각 페이지 어떻게 빈 프레임에 넣어줄지에 대하여 생각해보겠습니다.
아래와 같이 프로세스를 쪼갠 페이지의 갯수만큼 연속적인 공간의 프레임이 있다면 문제는 생기지 않을것입니다.

그런데 만약 연속적인 공간에 empty frame이 있는것이 아니라 아래와 같다면 어떨까요?
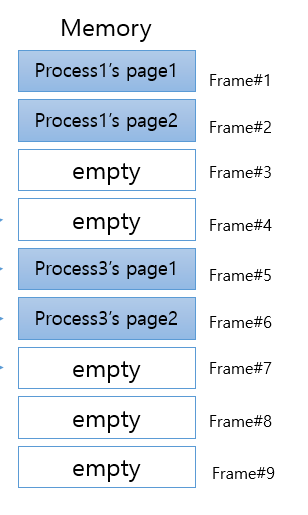
위와 같은 구조에서 프로세스2의 페이지들을 삽입한다면 아래와 같을것 같습니다.
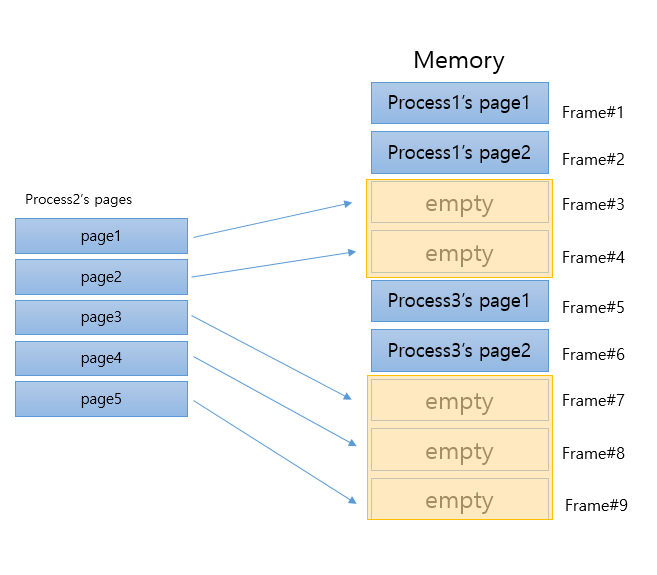
위처럼 페이지가 프레임에 들어간다면 알맞게 들어갈수 있습니다. 하지만 몇가지 문제가 발생할것 같습니다.
bounds register를 다룰 때 상대주소와 베이스 주소를 더한 값을 바운드와 비교한다했는데 프로세스3의 페이지들이 차지하는 영역 만큼 주소가 붕뜨게 될 것입니다. 즉, 바인딩의 문제가 생깁니다.
바인딩 문제가 무시된다고 해도 주소를 이용한 연산을 주로 사용하는 컴퓨터 체계에서 큰 오류를 범하게 됩니다.
만약 empty frame#4에 들어간 page2의 마지막 명령이 "다음번 주소에 있는 변수값을 참조해라"로 가정하겠습니다. 그렇다면 원래의 의도는 process2에 있는 page3에 존재하는 첫번째 주소값을 참조하려 했던것일것입니다.
하지만 의도와는 다르게 frame#5에 들어가있는 process3의 page1의 첫 주소값을 참조하여 연산이 크게 달라질 것입니다.
이러한 오류를 해결하기 위해서 어떻게 해야 하는지 이제부터 알아보겠습니다.
Addressing
따로따로 떨어진 프로세스의 덩어리를 참조하려면? 이 덩어리들에게도 번호를 매기는 것입니다. 번호가 없으니까 다음 페이지를 헷갈려서 이상한 다른 프로세스의 첫주소를 참조했겠죠! 만약 덩이리들에게 12345번을 매긴다면 페이지2번이 마지막에 다음 주소 참조라는 명령을 내려도 자동으로 2다음인 3번의 첫주소가 참조 되겠죠
이를 이제 주소체계내에서 말이되게 풀어나가보겠습니다.
8비트 주소체계는 2의 8승 이니 총 0번부터 255번까지의 주소를 사용할수 있습니다. 그런데 만약 페이지의 크기(프로세스를 조각낸 크기)가 64바이트라 가정한다면 2의8승 나누기 2의 6승인 2의2승 즉, 4만큼의 페이지 번호를 매길수 있습니다.
이렇게 나뉜 페이지들의 번호와 페이지안에 있는 내용을 page number와 page offset이라 칭합니다. 하지만 이는 프로세스를 잘게 쪼개어 논리적으로 나눈 번호와 조각들의 내용일것입니다. 실제 메모리에서는 이러한 정보를 잘 모르게 되죠 그렇다면 이 논리주소를 물리주소로 바꿔주는 매핑에서 문제가 발생할수 있지만 이를 방지하여 메모리에 잘 매핑될수 있게 해주는 것이 바로 페이지 테이블입니다.
페이지 테이블은 물리 메모리의 각 프레임의 시작 주소를 저장하고 있으며 이때 offset은 프레임 내에서의 주소로 사용됩니다. 이 페이지 테이블을 접근할때 사용하는것이 페이지 번호입니다.
페이지 테이블 = 페이지 번호(물리메모리, 각 프레임의 시작주소) + 페이지 옵셋
참 길게도 풀어썻는데 요점만! 아주 쉽게 비유 해보면! 따로 따로 나뉘어진 덩어리(페이지)들에 번호를 부여하고 이 번호와 따로 따로 떨어진 frame의 첫 주소를 매핑 해줌으로서 물리적인 비연속을 논리적으로 연속되게 붙여준다.
이들을 매핑해준 정보를 테이블로 나타낸것이 페이지 테이블이다.
그렇다면 실제 어드레스는(물리주소)
(페이지번호에 매핑된 프레임의 첫주소) X (옵셋의 크기) + (옵셋) 으로 구할수있습니다.
만약 프레임 번호가 0110 이고 옵셋이 11111111 이라하면 실제 어드레스는 011011111111이 되는것이죠
이렇게 되기 위해선 0110 + 11111111이 아닌 0110X옵셋의 크기(2의 m승) + 옵셋 을 계산해야합니다.
Segmentation
이제 길고 길었던 페이징을 다 다루고 다음 내용인 Segmentation에 들어왔습니다 근데 이친구도 만만치 않습니다. 중요합니다! <h1>태그입니다! 페이지랑 중요도는 똑같습니다!
지금까지 우리는 프로세스를 정해진 사이즈로 잘게잘게 쪼개어 메모리에 올리는 페이징을 알아보았습니다! 그런데! 프로세스를 자르는 크기를 고정하는 방법만 존재할까요? 적당한 로직을 대입하여 덩어리의 선언을 가변적으로 해주어도 될것같습니다. 그리고 이제부터 그 프로세스 조각들의 이름을 세그먼트라 해보겠습니다.
예를 들어 프로세스를 code + data + stack +heap 등으로 나누는 것 역시 세그먼테이션입니다 그런데 이들의 크기는 동일하지 않을것입니다. 특히 저와 같은 초짜 개발자는 코드내에서 불필요한 선언이나 로직을 돌려 리소스를 좀먹은 일명 똥...을 많이 만들어 내기때문에 실제로 코드영역은 짧아보여도 이 똥 코드로 인해 잡아먹히는 stack영역또는 heap영역은 방대해 질것입니다. 어쨋든! 좋은 예시는 아니지만 이처럼 프로세스의 조각의 크기를 가변적으로 사용하는것을 세그먼테이션(segmentation)이라 합니다.
-프로그램의 세그먼트들은 같은 크기를 갖지 않는다.
-세그먼트 각각의 최대 길이를 알고 있어야합니다.
-주소체계는 세그먼트 번호와 옵셋으로 구분합니다. Use SegmentNumber and offset
-내부 단편화(internal fragmentation)이 발생하지 않습니다.
만약 16비트 주소 체계 내에서 12비트를 offset으로 사용하고 있다면
segment를 가질수 있는 양은 2의 4승인 16개 입니다.
만약 위 시스템에서 16개의 세그먼트가 존재 한다면 한 세그먼트의 최대 크기는 2의12승 X 2인 4K입니다.
페이징의 경우 운영체제가 다 알아서 해주었습니다. 하지만 세그먼테이션의 경우 개발자가 한 세그먼트의 최댓값을 알고 있어야 합니다. 개발자에게 보이기 때문입니다.
스택오버플로우를 예로 들어보겠습니다. 개발자가 사용할수 있는 스택영역의 세그먼트는 제한적인데 지역변수를 많이 사용하거나 깊은영역의 재귀함수 호출로 인한 스택 사용등 사용가능한 최대 세그먼트 값을 넘어서게 되면 스택오버플로우가 발생하며 프로그램은 더이상 실행되지 못할것입니다.
페이징과 달리 세그먼트의 크기가 가변적으로 선언이 가능하다면 세그먼트의 번호는 그 자체가 첫주소인 인덱스가 될 것입니다. 논리적 주소값이 index + offset이 되겠네요!
이게 뭔 소리냐! 세그먼트 번화와 주소에 관련해서 2진수적인 개념을 불어 넣으면 안된다는것입니다.
1번 세그먼트의 길이가 4라면, 0,1,2,3번 주소를 사용할것이며
2번 세그먼트의 인덱스는 4가되고, 번호는 2번이지만 실제 인덱스값은 0100(십진수4)이겠죠! 이전 세그먼트 길이가 인덱스가 되는 원리 입니다.
하지만 이로워보이는 세그멘테이션 기법에도 치명적인 오류가 있습니다. 우리가 페이징기법을 사용하는 본질적인 이유가 외부단편화로 인한 컴팩션을 없애기 위해서였죠! 세그먼테이션 기법을 통해 가변적인 크기로 프로세스를 잘라서 물리적인 메모리에 올리다보면 크고작은 구멍이 생기게 될것입니다. 이러한 구멍때문에 컴팩션을 해주어야하는 상황이 발생하죠!
대부분의 유저는 여러 프로세스를 메모리에 많이 올리고 사용하는 멀티 프로세싱 환경을 선호합니다. 그래서 오늘날엔 세그먼테이션기법 보다 안정적인 페이징 기법이 상용화되었습니다.
긴글읽어주셔서 감사합니다. 제가 공부한 내용을 바탕으로 정리한 글이며, 제 이해를 바탕으로 포스팅했기때문에 틀린 내용일수 있습니다! 만약 오류가 있을시 댓글 부탁드립니다..! 수정하겠습니다
'Major > Operating System' 카테고리의 다른 글
| Operating System - Virtual memory (2) | 2021.05.30 |
|---|---|
| Operating System - Deadlock & Starvation (1) | 2021.05.29 |
| Operating System - Mutual Exclusion (1) | 2021.04.14 |
| Operating System - Treads (1) | 2021.04.14 |
| Operating System - process description & control (0) | 2021.04.14 |
